An example of reflectivity-based rain rate over-estimation due to ice hydrometeor contamination on 18 August 2009

Introduction

Historically, the measured radar reflectivity factor (Z) has been used to estimate the instantaneous rainfall rate. In developing these R(Z) relationships, it is assumed that a population of liquid raindrops is responsible for the backscattered signal received by the radar. This assumption is compromised when the pulse volume also contains frozen hydrometeors.

Freely falling raindrops generally become unstable and breakup as their diameters exceed ~8 mm. In contrast, the ice structure of graupel pellets and hailstones allows them to maintain much larger diameters. Since the strength of the backscattered signal is a strong function of the diameter of the scattering particle, the presence of frozen hydrometeors in the radar resolution volume generally increases reflectivity. This is especially true when the ice particles are undergoing melting and their refractive index values approach that of water. As a result, the rain rate calculated from the reflectivity factor is generally overestimated when ice particles “contaminate” the raindrop population. An example of this effect was observed by the CSU-CHILL radar on 18 August 2009.

Reflectivity

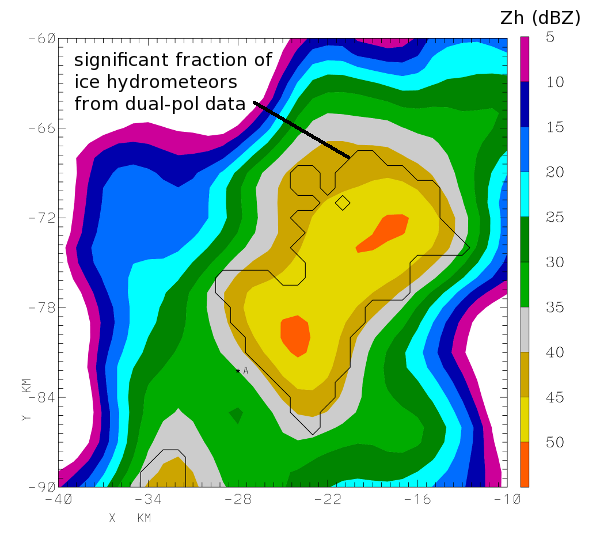
The following plot shows the radar reflectivity data recorded in a 0.6 degree PPI sweep made at 1920 UTC. To aid in contour plotting, the data have been interpolated to a 1 km X, Y Cartesian grid on the PPI scan surface. A 2-D horizontal smoother has been applied to the gridded data. The single black contour line encloses grid points where a fuzzy logic particle identification procedure has inferred the presence of a significant frozen hydrometeor component.

R(Z) Rain Rate

Rain rates calculated from the basic reflectivity data are shown below. This calculation was done using the standard NWS / WSR-88D equation:

$R=0.017Z^{0.714}$ (R in mm/hr, Z in $\mathrm {mm} ^{6}/\mathrm {m} ^{3}$; with the maximum Z value clamped at the linear scale equivalent of 53 dBZ)

For reference, this formula yields a rain rate of 63 $\mathrm {mm/hr}$ for a reflectivity factor of 50 dBZ.

Specific Differential Propagation Phase

Dual polarization radars can make measurements that are more directly associated with the raindrop component of the scatters in the pulse volume. One such measurement is Specific differential propagation phase ($K_{dp}$).

$K_{dp}$ is the rate at which the phase difference between the horizontally and vertically polarized received signals changes per km range interval along the beam path. In areas where a high concentration of oblate particles exist (i.e., large raindrops), the phase of the horizontally-polarized (H) radar pulse will increasingly lag that of the V pulse. Ice particles are generally more spherically shaped than large raindrops and they typically do not maintain predictable orientations as they fall. Due to these factors, the frozen hydrometeor component in convective rain minimally affects $K_{dp}$.

The $K_{dp}$ values developed using the CSU DROPS (Dualpol Radar Operational Products System) procedures are shown in the next plot. In this case, the $K_{dp}$ magnitudes are only a fraction of a degree / km, indicating that only a limited portion of the backscattered signal amplitude is due to oblate particles (raindrops).

R($K_{dp}$)

Various power law relationships have been developed to estimate rain rate from $K_{dp}$. The final plot shows such rain rates calculated from:

$R=40.5Kdp^{0.85}$ ($K_{dp}$ is one way differential propagation phase shift in $\mathrm {deg/km}$)

These phase-based rain rates are generally under 20 mm / hr, compared to rain rate peaks exceeding 60 mm / hr for the basic reflectivity method.

A simple method of rain rate validation was developed by examining the tipping rates of four Denver Urban Drainage and Flood Control District rain gauges that were located within the 40 dBZ reflectivity contour at 1920 UTC. At this single time snapshot, the reflectivity-based rain rates all exceeded the gauge-reported rates while the $K_{dp}$ based rates were all less than the measured surface rates. When compared to the surface rates, the average error in the reflectivity-estimated rates was +18 mm / hr. The $K_{dp}$-based average rate error was -13 mm / hr.

Conclusion

The reduced sensitivity to the effects of ice contamination is one of the advantages of using dual polarization radar technology for the remote sensing of rainfall.

External Links

Denver Urban Drainage and Flood Control District